パルマーペンギンデータセットを例にPyTorchの使い方を学ぼう#
ニューラルネットワークの実装のためのライブラリ「PyTorch」の使い方を,penguinデータセットのクラス分類を例に学ぼう.
import torch
import torch.nn as nn
import torch.nn.functional as F
from sklearn.preprocessing import StandardScaler
import pandas as pd
import numpy as np
import random
import os
SEED = 20220725
# seed function for reproducibility
def set_seed(seed: int=0):
random.seed(seed)
np.random.seed(seed)
os.environ["PYTHONHASHSEED"] = str(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
set_seed(SEED)
SECTION 1 : 学習用データのロードとセットアップ#
オリジンデータをもとに2つのファイルに分けたデータセット 。
penguin-clean-train.csv = 学習用データセット、オリジナルデータから70%使用。
penguin-clean-test.csv = テスト用データセット、オリジナルデータから30%抽出
SECTION 1 : Load and setup data for training
the datasets separated in two files from originai datasets:
penguin-clean-train.csv = datasets for training purpose, 70% from the original data
penguin-clean-test.csv = datasets for testing purpose, 30% from the original data
Section 1.1 Data Loading#
データセットは前処理済みのものが既にあるので、これを直接利用する rianrajagede/penguin-python
en2ja = {
"species": "ペンギンの種類",
"island": "生息する島",
"bill_length_mm": "クチバシの長さ",
"bill_depth_mm":"クチバシの厚み",
"flipper_length_mm": "翼の長さ",
"body_mass_g": "体重",
"sex": "性別",
"year": "調査年",
}
#load
dataset_url = "https://raw.githubusercontent.com/rianrajagede/penguin-python/master/Datasets/penguins-clean-all.csv"
training_url = "https://raw.githubusercontent.com/rianrajagede/penguin-python/master/Datasets/penguins-clean-train.csv"
test_url = "https://raw.githubusercontent.com/rianrajagede/penguin-python/master/Datasets/penguins-clean-test.csv"
# datatrain = pd.read_csv('../Datasets/penguins-clean-train.csv')
df_train = pd.read_csv(training_url)
df_train.shape
(240, 5)
df_train_ja = df_train.copy()
df_train_ja.columns = [en2ja[key] for key in df_train_ja.columns]
df_train_ja
| ペンギンの種類 | クチバシの長さ | クチバシの厚み | 翼の長さ | 体重 | |
|---|---|---|---|---|---|
| 0 | Gentoo | 46.2 | 14.5 | 209 | 4800 |
| 1 | Gentoo | 43.6 | 13.9 | 217 | 4900 |
| 2 | Gentoo | 45.3 | 13.7 | 210 | 4300 |
| 3 | Gentoo | 53.4 | 15.8 | 219 | 5500 |
| 4 | Adelie | 40.6 | 18.8 | 193 | 3800 |
| ... | ... | ... | ... | ... | ... |
| 235 | Gentoo | 46.8 | 15.4 | 215 | 5150 |
| 236 | Gentoo | 46.6 | 14.2 | 210 | 4850 |
| 237 | Gentoo | 43.5 | 14.2 | 220 | 4700 |
| 238 | Gentoo | 46.9 | 14.6 | 222 | 4875 |
| 239 | Chinstrap | 50.7 | 19.7 | 203 | 4050 |
240 rows × 5 columns
#Section 1.2 Preprocessing
#change string value to numeric
df_train.loc[df_train['species']=='Adelie', 'species']=0
df_train.loc[df_train['species']=='Gentoo', 'species']=1
df_train.loc[df_train['species']=='Chinstrap', 'species']=2
df_train = df_train.apply(pd.to_numeric)
#change dataframe to array
df_array = df_train.values
#split x and y (feature and target)
X_train = df_array[:,1:]
y_train = df_array[:,0]
#standardize
#palmer-penguin dataset has varying scales
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
SECTION 2 : モデルの構築と学習#
隠れ層を1層持つ、多層パーセプトロンモデル。
入力層:4ニューロン、Palmer Penguinデータセットからの特徴を表す。
隠れ層:20ニューロン、ReLUで活性化
出力層:3ニューロン、種の数を表す、Softmax Layer
最適化器 = 確率的勾配降下法、バッチサイズなし
損失関数 = カテゴリクロスエントロピー
学習率 = 0.01
エポック = 50
SECTION 2 : Build and Train Model
Multilayer perceptron model, with one hidden layer.
input layer : 4 neuron, represents the feature from Palmer Penguin dataset
hidden layer : 20 neuron, activation using ReLU output layer : 3 neuron, represents the number of species, Softmax Layer optimizer = stochastic gradient descent with no batch-size
loss function = categorical cross entropy
learning rate = 0.01 #hyperparameters hl = 20 lr = 0.01 num_epoch = 100
epoch = 50
#hyperparameters
hl = 20
lr = 0.01
num_epoch = 100
ネットワークはnn.Sequentialを使って作るパターンと,nn.Moduleを継承したクラスを作るパターンがある.
mynet = nn.Sequential(
nn.Linear(4, 20,),
nn.ReLU(),
nn.Linear(20, 3),
nn.Softmax(dim=1)
)
#build model
class Net(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(4, hl)
self.fc2 = nn.Linear(hl, 3)
def forward(self, x):
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
net = Net()
#choose optimizer and loss function
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(net.parameters(), lr=lr)
X_train = torch.from_numpy(X_train).float()
y_train = torch.from_numpy(y_train).long()
print("training data:",type(X_train), X_train.shape, X_train.dtype)
print("test data:", type(y_train), y_train.shape, y_train.dtype)
training data: <class 'torch.Tensor'> torch.Size([240, 4]) torch.float32
test data: <class 'torch.Tensor'> torch.Size([240]) torch.int64
net.eval()
print(net.training
)
net.train()
print(net.training
)
False
True
訓練ループ
# logging
logs = {"loss":[], "acc":[]}
#train
if torch.cuda.is_available():
net = net.to("cuda:0")
X_train = X_train.to("cuda:0")
y_train = y_train.to("cuda:0")
for epoch in range(num_epoch):
#feedforward - backprop
# 勾配の初期化
optimizer.zero_grad()
# フォワードプロップ。順伝搬
out = net(X_train)
# 損失関数の計算
loss = criterion(out, y_train)
# 逆伝搬して、各パラメータの勾配を求める
loss.backward()
# 勾配を使って学習可能パラメータの値を更新
optimizer.step()
with torch.no_grad():
acc = 100 * torch.sum(y_train==torch.max(out.data, 1)[1]).double() / len(y_train)
print ('Epoch [%d/%d] Loss: %.4f Acc: %.4f'
%(epoch+1, num_epoch, loss.item(), acc.item()))
# logging
logs["loss"] += [loss.cpu().detach().item()]
logs["acc"] += [acc.cpu().detach().item()]
Epoch [1/100] Loss: 1.1014 Acc: 42.9167
Epoch [2/100] Loss: 1.0938 Acc: 44.1667
Epoch [3/100] Loss: 1.0864 Acc: 46.2500
Epoch [4/100] Loss: 1.0790 Acc: 49.1667
Epoch [5/100] Loss: 1.0718 Acc: 51.6667
Epoch [6/100] Loss: 1.0646 Acc: 52.5000
Epoch [7/100] Loss: 1.0575 Acc: 55.4167
Epoch [8/100] Loss: 1.0505 Acc: 55.4167
Epoch [9/100] Loss: 1.0436 Acc: 59.1667
Epoch [10/100] Loss: 1.0367 Acc: 60.4167
Epoch [11/100] Loss: 1.0300 Acc: 62.5000
Epoch [12/100] Loss: 1.0233 Acc: 66.2500
Epoch [13/100] Loss: 1.0167 Acc: 67.5000
Epoch [14/100] Loss: 1.0102 Acc: 68.3333
Epoch [15/100] Loss: 1.0037 Acc: 70.4167
Epoch [16/100] Loss: 0.9973 Acc: 71.2500
Epoch [17/100] Loss: 0.9910 Acc: 72.9167
Epoch [18/100] Loss: 0.9848 Acc: 73.7500
Epoch [19/100] Loss: 0.9786 Acc: 74.1667
Epoch [20/100] Loss: 0.9725 Acc: 75.8333
Epoch [21/100] Loss: 0.9664 Acc: 75.8333
Epoch [22/100] Loss: 0.9604 Acc: 76.2500
Epoch [23/100] Loss: 0.9545 Acc: 76.2500
Epoch [24/100] Loss: 0.9486 Acc: 76.2500
Epoch [25/100] Loss: 0.9428 Acc: 77.0833
Epoch [26/100] Loss: 0.9371 Acc: 77.5000
Epoch [27/100] Loss: 0.9314 Acc: 77.9167
Epoch [28/100] Loss: 0.9257 Acc: 77.9167
Epoch [29/100] Loss: 0.9202 Acc: 78.3333
Epoch [30/100] Loss: 0.9146 Acc: 78.3333
Epoch [31/100] Loss: 0.9092 Acc: 78.3333
Epoch [32/100] Loss: 0.9038 Acc: 78.3333
Epoch [33/100] Loss: 0.8984 Acc: 78.3333
Epoch [34/100] Loss: 0.8931 Acc: 78.3333
Epoch [35/100] Loss: 0.8878 Acc: 78.3333
Epoch [36/100] Loss: 0.8826 Acc: 78.3333
Epoch [37/100] Loss: 0.8775 Acc: 78.3333
Epoch [38/100] Loss: 0.8723 Acc: 78.3333
Epoch [39/100] Loss: 0.8673 Acc: 78.7500
Epoch [40/100] Loss: 0.8623 Acc: 78.7500
Epoch [41/100] Loss: 0.8573 Acc: 78.7500
Epoch [42/100] Loss: 0.8524 Acc: 78.7500
Epoch [43/100] Loss: 0.8475 Acc: 78.7500
Epoch [44/100] Loss: 0.8427 Acc: 78.7500
Epoch [45/100] Loss: 0.8379 Acc: 78.7500
Epoch [46/100] Loss: 0.8331 Acc: 79.1667
Epoch [47/100] Loss: 0.8284 Acc: 79.1667
Epoch [48/100] Loss: 0.8238 Acc: 79.1667
Epoch [49/100] Loss: 0.8192 Acc: 79.1667
Epoch [50/100] Loss: 0.8146 Acc: 79.1667
Epoch [51/100] Loss: 0.8101 Acc: 79.5833
Epoch [52/100] Loss: 0.8056 Acc: 79.5833
Epoch [53/100] Loss: 0.8012 Acc: 80.0000
Epoch [54/100] Loss: 0.7968 Acc: 80.0000
Epoch [55/100] Loss: 0.7924 Acc: 80.0000
Epoch [56/100] Loss: 0.7881 Acc: 80.0000
Epoch [57/100] Loss: 0.7838 Acc: 80.0000
Epoch [58/100] Loss: 0.7795 Acc: 80.0000
Epoch [59/100] Loss: 0.7753 Acc: 80.0000
Epoch [60/100] Loss: 0.7712 Acc: 80.0000
Epoch [61/100] Loss: 0.7670 Acc: 80.0000
Epoch [62/100] Loss: 0.7629 Acc: 80.0000
Epoch [63/100] Loss: 0.7589 Acc: 80.0000
Epoch [64/100] Loss: 0.7548 Acc: 80.0000
Epoch [65/100] Loss: 0.7508 Acc: 80.0000
Epoch [66/100] Loss: 0.7469 Acc: 80.0000
Epoch [67/100] Loss: 0.7430 Acc: 80.0000
Epoch [68/100] Loss: 0.7391 Acc: 80.0000
Epoch [69/100] Loss: 0.7352 Acc: 80.0000
Epoch [70/100] Loss: 0.7314 Acc: 80.0000
Epoch [71/100] Loss: 0.7276 Acc: 80.0000
Epoch [72/100] Loss: 0.7239 Acc: 80.0000
Epoch [73/100] Loss: 0.7202 Acc: 80.0000
Epoch [74/100] Loss: 0.7165 Acc: 80.0000
Epoch [75/100] Loss: 0.7128 Acc: 80.0000
Epoch [76/100] Loss: 0.7092 Acc: 80.0000
Epoch [77/100] Loss: 0.7056 Acc: 80.0000
Epoch [78/100] Loss: 0.7021 Acc: 80.0000
Epoch [79/100] Loss: 0.6985 Acc: 80.0000
Epoch [80/100] Loss: 0.6950 Acc: 80.0000
Epoch [81/100] Loss: 0.6916 Acc: 80.0000
Epoch [82/100] Loss: 0.6882 Acc: 80.0000
Epoch [83/100] Loss: 0.6847 Acc: 80.0000
Epoch [84/100] Loss: 0.6814 Acc: 80.0000
Epoch [85/100] Loss: 0.6780 Acc: 80.0000
Epoch [86/100] Loss: 0.6747 Acc: 80.0000
Epoch [87/100] Loss: 0.6714 Acc: 80.0000
Epoch [88/100] Loss: 0.6682 Acc: 80.0000
Epoch [89/100] Loss: 0.6650 Acc: 80.0000
Epoch [90/100] Loss: 0.6618 Acc: 80.0000
Epoch [91/100] Loss: 0.6586 Acc: 80.0000
Epoch [92/100] Loss: 0.6555 Acc: 80.0000
Epoch [93/100] Loss: 0.6523 Acc: 80.0000
Epoch [94/100] Loss: 0.6493 Acc: 80.0000
Epoch [95/100] Loss: 0.6462 Acc: 80.0000
Epoch [96/100] Loss: 0.6432 Acc: 80.0000
Epoch [97/100] Loss: 0.6402 Acc: 80.0000
Epoch [98/100] Loss: 0.6372 Acc: 80.0000
Epoch [99/100] Loss: 0.6342 Acc: 80.0000
Epoch [100/100] Loss: 0.6313 Acc: 80.0000
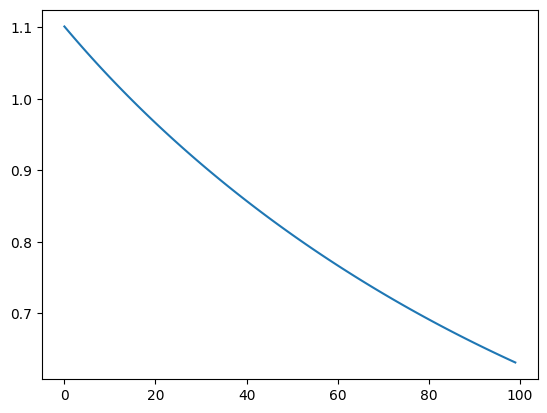
学習中の損失関数のモニタリング
pd.DataFrame(logs)["loss"].plot()
<Axes: >
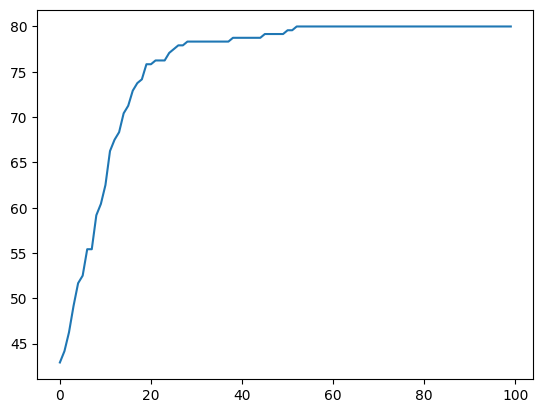
学習中の正答率のモニタリング
pd.DataFrame(logs)["acc"].plot()
<Axes: >
SECTION 3 : モデルの評価#
#load
df_test = pd.read_csv(test_url)
#change string value to numeric
df_test.loc[df_test['species']=='Adelie', 'species']=0
df_test.loc[df_test['species']=='Gentoo', 'species']=1
df_test.loc[df_test['species']=='Chinstrap', 'species']=2
df_test = df_test.apply(pd.to_numeric)
#change dataframe to array
df_test_array = df_test.values
#split x and y (feature and target)
X_test = df_test_array[:,1:]
y_test = df_test_array[:,0]
#standardization
X_test = scaler.transform(X_test)
#get prediction
X_test = torch.Tensor(X_test).float()
y_test = torch.Tensor(y_test).long()
# 必要ならばCPUからGPUへ配列を移動
#X_test = X_test.to(X_train.device)
#y_test = y_test.to(y_train.device)
if torch.cuda.is_available():
X_test = X_test.cuda()
y_test = y_test.cuda()
#テストデータに対するクラスラベルの予測
out = net.forward(X_test)#.softmax(1)
_, predicted = torch.max(out.data, 1)
#get accuration
print('Accuracy of the network %.4f %%' % (100 * torch.sum(y_test==predicted).double() / len(y_test)))
Accuracy of the network 80.3922 %
[課題1] 入力層の次元数と隠れ層の次元数とクラス数を__init__の引数で変更できるようにNetクラスを修正せよ。#
Show code cell source
class FixedNet(nn.Module):
def __init__(self, num_features, hidden_size, num_class):
super().__init__()
self.fc1 = nn.Linear(num_features, hidden_size)
self.fc2 = nn.Linear(hidden_size, num_class)
def forward(self, x):
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
num_features = X_train.shape[1]
hidden_size = 100
num_class = 3
fixed_net = FixedNet(num_features,hidden_size, num_class)
fixed_net
FixedNet(
(fc1): Linear(in_features=4, out_features=100, bias=True)
(fc2): Linear(in_features=100, out_features=3, bias=True)
)
[課題2] 課題1で作ったクラスを使って,クラス数をそのままに隠れ層の次元数を100にして200エポック訓練せよ.また,その際のtestデータの正答率を示せ.この際、set_seedを使いSEEDを1111に固定する事.#
Show code cell source
set_seed(1111)
net = FixedNet(num_features,hidden_size, num_class)
#choose optimizer and loss function
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(net.parameters(), lr=lr)
# 訓練のコード
# 評価のコード
[課題3] ペンギンデータのクラス分類を行うニューラルネットワークを作れ。ただし、ニューラルネットワークの隠れ層は5層で、それぞれが100次元のネットワークを作成せよ。また、このニューラルネットワークの活性化関数はすべてtanhである。この隠れ層をまとめたsequentialをfeature_extractorという変数にせよ。出力層は3クラス分類を行うために次元数は3にする。#
class TanhNet(nn.Module):
def __init__(self, hidden_size=100, n_class=3):
super().__init__()
self.feature_extractor = nn.Sequential(
nn.Linear(4, hidden_size), # 1
nn.Tanh(),
nn.Linear(hidden_size, hidden_size), # 2
nn.Tanh(),
... # 3
... # 4
... # 5
)
self.classifier = nn.Linear(hidden_size, n_class)
def forward(self,x):
x = self.feature_extractor(x)
return self.classifier(x)
Cell In[19], line 9
... # 3
^
SyntaxError: invalid syntax. Perhaps you forgot a comma?
a = TanhNet()
#a(X_train.cpu())
a
TanhNet(
(feature_extractor): Sequential(
(0): Linear(in_features=4, out_features=100, bias=True)
(1): Tanh()
(2): Linear(in_features=100, out_features=100, bias=True)
(3): Tanh()
)
(classifier): Linear(in_features=100, out_features=3, bias=True)
)


