ロジスティック回帰 (Logistic Regression)

ロジスティック回帰 (Logistic Regression)#

import numpy as np 
import pandas as pd 

import plotly.express as px
from plotly.subplots import make_subplots
import plotly.figure_factory as ff
import plotly.graph_objects as go
import plotly.io as pio

import warnings
warnings.filterwarnings('ignore')

はじめに#

このノートでは二値分類に利用される「ロジスティック回帰」について勉強します。
まずはロジスティック回帰の中で利用されるロジスティック関数について復習し、その後、ロジスティック回帰とはどのようなものなのかを紹介します。

そもそもロジスティック関数とは#

ロジスティック関数 ($\sigma:\mathbb{R}\rightarrow (0,1)$):

\[ \sigma(x,a) := \frac{1}{1+\exp (-ax)} \text {. } \]

ロジスティック関数をPythonで実装すると、以下の様になります。

def logistic_sigmoid(x:np.array, a:float=1.0)->float:
    """
    x: Iput
    a: Gain
    """
    #assert a>0.0, "Gain `a` must be greater than 0."
    return 1.0 / (1.0 + np.exp(-a*x))

また、ロジスティック関数の返り値がどのようなグラフを描くのかを確認してみましょう。
ここでは作図にplotlyを利用したので、グラフの表示範囲を自分で変更して観察してください。

x = np.linspace(-20,20, 50)
y = logistic_sigmoid(x, a=1)
sample_df = pd.DataFrame({"Input x":x, 
                          "Output y": y})

logistic_sigmoid_fig = px.line(data_frame=sample_df, 
                               x="Input x",y="Output y", 
                               width=800, height=800, 
                               markers=True,
                               title="Logistic Sigmoid Function"
                              )
logistic_sigmoid_fig.show()

ここでロジスティック関数と呼んでいる関数にはaという引数があります。この値はgainを示していて、上のプロットは$a=1$の場合のものです。
この$a=1$の特殊な状態のとき、「標準シグモイド関数」または「標準ロジスティック関数: Standard logistic function」と呼ばれます。
また機械学習の分野ではこの標準シグモイド関数を単に「シグモイド関数」と呼ぶ事が多いです。
(参考: https://atmarkit.itmedia.co.jp/ait/articles/2003/04/news021.html)

「シグモイド」とは「ギリシア語のシグマの語末形（アルファベットでいうとS）に似た形」を表す言葉なので、ロジスティック・シグモイド関数以外にもシグモイド関数は存在します。しかしそれでも機械学習の分野では、標準シグモイド関数を単にシグモイド関数と呼びます（実際それ以外の呼び方をしている人を見たことがない…）

(参考: https://kenichia.hatenablog.com/entry/2017/03/04/122551)

gainはグラフのS字カーブをきつくしたり、ゆるくしたりするためのパラメータとして機能します。
実際に以下のプロットで、gain aスライダーを操作して確認してみましょう。
gainが0に近い時はx軸に平行に近い直線のような形を取り、gainを徐々に大きくするとS字になっていきます。更にgainを大きくするとS字の勾配が大きくなり、最終的にステップ関数に近い形になることがわかります。

ロジスティック回帰とは#

ロジスティック回帰（Logistic Regression）とは、__目的変数（ラベル,label,予測したい値のこと）$y$ が2値データ（バイナリデータ, binary data, 例えば$y=0,1$）の場合、実数値を取る目的変数$x$に対する予測モデルの一種です。

例として、ある数値レベル$x$について個体が反応したら$y=1$、無反応なら$y=0$と対応された$N$組のデータが観測されたとします。

\[ \left(x^{(1)}, y^{(1)}\right),\left(x^{(2)}, y^{(2)}\right), \ldots,\left(x^{(n)}, y^{(n)}\right),\ldots,\left(x^{(N)}, y^{(N)}\right) \]

\[\begin{split} x^{(n)} \in \mathbb{R}, \quad y^{(n)}= \begin{cases}1, & \text { (positive) } \\ 0, & \text { (negative) }\end{cases} \end{split}\]

何個目の組のペアなのかを数式上で分かりやすくするために、各変数の肩に組番号を書いています。

このようなバイナリの目的変数に対して、数値レベル$x$に対する反応確率$p$を推定するモデルの構築を考えましょう。ここで、反応したかを表す確率変数$Y$を導入すると、数値レベル$x$に対する反応確率は$\operatorname{P}(Y=1|x)=p$と表され、非反応確率は$\operatorname{P}(Y=0|1)=1-p$と表されます。モデルを構築するためには、反応確率$p$の関数の形を考える必要があります。$p$は確率ですから、取り得る範囲は$0\leq p \leq 1$となります。また、反応を引き起こす要因$x$は実数値$-\infty \leq x \leq \infty$です。

このような$x$と$p$を結びつける関数として、ロジスティック関数$\sigma(\cdot)$を用いるのが「ロジスティックモデル」です。すなわち、ロジスティックモデルでは反応確率$p$はパラメータ$w_0, w_1$を用いて、次の用に表されます。

\[ p= \sigma\left(w_{0}+w_{1} x\right)=\frac{1}{1+\exp \left[-\left(w_{0}+w_{1} x\right)\right]} \]

\[ (0 \leq p \leq 1), \quad(-\infty<x<\infty) \]

観測された$n$組のデータに基づいてパラメータ$w_0, w_1$の値を推定すれば、任意の数値レベル$x$に対して反応する確率を出力するモデルが定まります。ここではパラメータを$w_0,w_1$としていますが、$w_0$はNeural Networkでよく見かけるbiasの役割を果たします。

ロジスティックモデルの推定#

上記では一種類の説明変数$x$に関する記述でしたが、もう少し一般的に、$F$個の説明変数に対して目的変数$y$が従う確率の推定を考えます。今、$F$個の説明変数$ x_{1}, x_{2}, \ldots, x_{F}$と目的変数$y$について、観測された$n$番目のデータを

\[\begin{split} \begin{array}{r} \left(x_{1}^{(n)}, x_{2}^{(n)}, \ldots, x_{F}^{(n)}\right), \quad y^{(n)}= \begin{cases}1, & (\text { positive) } \\ 0, & \text { (negative) }\end{cases} \\ (n=1,2, \ldots, N) . \end{array} \end{split}\]

とします。先程と同様に確率変数$Y$を導入すると、反応確率、非反応確率はそれぞれ

\[ \operatorname{P}\left(Y=1 \mid x_{1}, \ldots x_{F}\right)=p, \quad \operatorname{P}\left(Y=0 \mid x_{1}, \ldots x_{F}\right)=1-p \]

となり、そして説明変数$ x_{1}, x_{2}, \ldots, x_{F}$と反応確率$p$との関係を

\[\begin{split} \begin{aligned} p &=\frac{1}{1+\exp \left[-\left(w_{0}+w_{1} x_{1}+w_{2} x_{2}+\cdots+w_{F} x_{F}\right)\right]} \\ &=\frac{1}{1+\exp \left[-\sum_{n=1}^{N}{\left(w_n x_n\right)} - w_0\right]} \\ &=\frac{1}{1+\exp \left(-\boldsymbol{w}^{\top} \boldsymbol{x}\right)} \\ &=\sigma({\boldsymbol{w}^{\top} \boldsymbol{x}})\label{eq:proj} \end{aligned} \end{split}\]

によって結びつけます。ここで、$\boldsymbol{w},\boldsymbol{x}$はそれぞれ以下の通りです。

\[\begin{split} \boldsymbol{w} = (w_0, w_1, \dots, w_F)^\mathsf{T} = \left( \begin{array}{c} w_0 \\ w_1 \\ \vdots \\ w_F \end{array} \right) \end{split}\]

\[\begin{split} \boldsymbol{x} = (1, x_1, x_2, \dots, x_F)^\mathsf{T} = \left( \begin{array}{c} 1 \\ x_1 \\ \vdots \\ x_F \end{array} \right) \end{split}\]

ロジスティック回帰のモデルを、ニューラルネットワークの様に表すと以下のようになります。（図中で使われている記号が、今回の解説で利用しているものと異なります。参考程度に見てください。）
(参考: https://www.hellocybernetics.tech/entry/2016/05/22/215529)

よって先程示した反応確率、非反応確率はそれぞれ以下のように書けますね。

\[ \operatorname{P}\left(Y=1 \mid \boldsymbol{w} ,\boldsymbol{x} \right)=p, \quad \operatorname{P}\left(Y=0 \mid \boldsymbol{w} ,\boldsymbol{x} \right)=1-p \]

ここでは観測された$N$組のデータに基づいてパラメータベクトル$\boldsymbol{w}$の値を推定しましょう。最尤法を用いてパラメータ推定を行う事を考えます。

今、$n$番目のデータに関しては、反応したか否かを示す確率変数$Y^{(n)}$と実現値$y^{(n)}$の組からなります。そこで、$n$番目のデータに対する真の反応確率を$p^{(n)}$とすると、反応確率、非反応確率はそれぞれ次のようになります。

\[ \operatorname{P}\left(Y^{(n)}=1\right)=p^{(n)}, \quad \operatorname{P}\left(Y^{(n)}=0\right)=1-p^{(n)} \]

上の式を見ると、この問題は歪なコインの問題であることが想像できますね。

※離散確率分布の相互関係

ピンクの線が多次元変数への一般化で、オレンジの線が複数回の試行を行った場合に対する一般化です。グレーの点線矢印は、それぞれの確率分布に対する共役の関係性を示しています（矢印の元に当たるのが共役事前分布（conjugate prior）です）。
(引用: ややこしい離散分布に関するまとめ - 作って遊ぶ機械学習。 https://machine-learning.hatenablog.com/entry/2016/03/26/211106 )

つまり、確率変数$Y^{(n)}$が従う確率分布は次のベルヌーイ分布である事がわかります。

\[\begin{split} \begin{aligned} \operatorname{P}\left(Y^{(n)}=y^{(n)}\right) &=\operatorname{Bern}\left(y^{(n)} \mid p^{(n)}\right) \\ &=\left(p^{(n)}\right)^{y^{(n)}}\left(1-p^{(n)}\right)^{1-y^{(n)}} \\ \end{aligned} \end{split}\]

\[ \left(y^{(n)}=0,1\right), (i=1,2, \ldots, N) \]

従って、$y^{(1)}, y^{(2)}, \dots, y^{(N)}$という$N$回の試行に基づく尤度関数は、サンプリングされた学習データの独立性（i.i.d標本）より、次式となります。

\[\begin{split} \begin{align} L(p^{(1)}, p^{(2)}, \dots, p^{(N)}) &= \prod_{n=1}^N {\rm Bern}(y^{(n)}|p^{(n)}) \\ &= \prod_{n=1}^N (p^{(n)})^{y^{(n)}} (1 – p^{(n)})^{1-y^{(n)}}.\label{eq:likelihood} \end{align} \end{split}\]

$p$はパラメータベクトル$\boldsymbol{w}$と説明変数$\boldsymbol{x}$の関数であり、学習可能なパラメータは$\boldsymbol{w}$でした。よってこの$p$を含む尤度関数$L$はパラメータ$\boldsymbol{w}$の関数である事がわかります。

この尤度を最大とするパラメータが、求めたい推定値$\boldsymbol{w}^*$です。そこで、対数尤度を最大化するようにパラメータ$\boldsymbol{w}$を決定しましょう。

\[\begin{split} \begin{align} \boldsymbol{w}^* &= \operatorname{argmax}_{\boldsymbol{w}}\left[ \log L(p^{(1)}, p^{(2)}, \dots, p^{(N)})\right] \\ &= \operatorname{argmax}_{\boldsymbol{w}}\left[ \log\{ \prod_{n=1}^N (p^{(n)})^{y^{(n)}} (1 – p^{(n)})^{1-y^{(n)}} \} \right]\\ &= \operatorname{argmax}_{\boldsymbol{w}}\left[ \sum_{n=1}^N \log\{ (p^{(n)})^{y^{(n)}} (1 – p^{(n)})^{1-y^{(n)}} \}\right] \ \because \textstyle (\log\prod_n c_n = \sum_n \log c_n) \\ &= \operatorname{argmax}_{\boldsymbol{w}}\left[ \sum_{n=1}^N \{ y^{(n)}\log p^{(n)} + (1-y^{(n)})\log (1 – p^{(n)}) \} \right]\\ &= \operatorname{argmin}_{\boldsymbol{w}}\left[ -\sum_{n=1}^N \{ y^{(n)}\log p^{(n)} + (1-y^{(n)})\log (1 – p^{(n)}) \}\right].\label{eq:loglike} \end{align} \end{split}\]

最終行でマイナスをつけているので、上は最小化問題に変化していることに注意してください。

最終行の項を$J(\boldsymbol{w})$と置くことにします。

\[ \begin{align*} J(\boldsymbol{w}) := -\sum_{n=1}^N \{ y^{(n)}\log p^{(n)} + (1-y^{(n)})\log (1 – p^{(n)}) \} \end{align*} \]

またこの$J(\boldsymbol{w})$のような、モデルのパラメータを訓練するために値を小さくしたい関数を損失関数（Loss Function）、または目的関数（Objective Function）と呼びます。

x = np.linspace(0,10, 50)
sample_df = pd.DataFrame({"W^T・x":x, 
                          "CrossEntropy": np.log(1 + np.exp(-x)),
                         })

likelihood_fig = px.line(data_frame=sample_df, 
                               x="W^T・x",y="CrossEntropy", 
                               width=800, height=800, 
                               markers=True,
                               title="J(w)の第二項について"
                              )
likelihood_fig.show()

上記より、$J(\boldsymbol{w})$を最小とする$\boldsymbol{w}$こそが求めたい推定値$\boldsymbol{w}^*$です。

\[ \boldsymbol{w}^* = \operatorname{argmin}_{\boldsymbol{w}}\left[ J(\boldsymbol{w}) \right] \]

さて、推定値$\boldsymbol{w}$を解析的に陽に表現する事は難しいです。この場合、ニュートン-ラフソン法や最急降下法などの方法で推定値を求める事が可能です。ここでは、今後のニューラルネットワークの解説へ繋げるために、最急降下法を用いることにします。

最急降下法では、ランダムにパラメータの初期値$\boldsymbol{w}^{[0]}$を設定し、下記のように微分によるマイナスをつけた下降方向にパラメータを更新していきます。

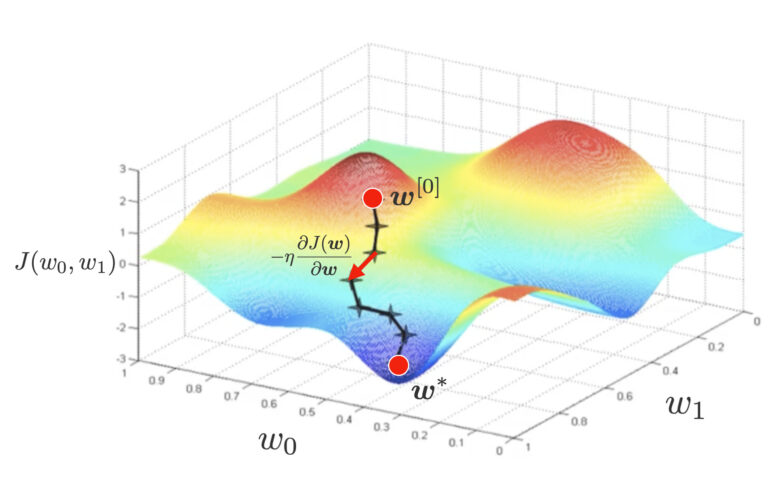
\[ \boldsymbol{w}^{[t+1]} = \boldsymbol{w}^{[t]} – \eta\frac{\partial J(\boldsymbol{w})}{\partial \boldsymbol{w}}. \]

▲最急降下法のイメージ。ちょっとずつ$w$の値を更新し、損失関数$J$の谷を探す

最適なモデルパラメータの計算#

$\require{cancel}$

偏微分$\frac{\partial J(\boldsymbol{w})}{\partial \boldsymbol{w}}$の値を計算するために、$J(\boldsymbol{w})$を整理します。

\[\begin{split} \begin{align*} J(\boldsymbol{w}) &= \sum_{n=1}^N [ -y^{(n)}\log p^{(n)} – (1-y^{(n)})\log (1 – p^{(n)}) ] \\ &\,\downarrow \textstyle{(p^{(n)} = \frac{1}{1+\exp(-\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)})}\text{を代入})} \\ &= \sum_{n=1}^N \biggl[-y^{(n)}\underbrace{\log (\frac{1}{1+\exp(-\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)})})}_{=\log1 – \log(1+\exp(-\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)}))} – (1-y^{(n)})\underbrace{\log (\frac{\exp(-\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)})}{1+\exp(-\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)})})}_{=-\boldsymbol{w}^\mathsf{T}\boldsymbol{x}^{(n)} – \log (1 + \exp(-\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)}))} \biggr] \\ &= \sum_{n=1}^N [y^{(n)}\log(1+\exp(-\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)})) + (1-y^{(n)})\{\boldsymbol{w}^\mathsf{T}\boldsymbol{x}^{(n)} + \log (1 + \exp(-\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)})) \} ] \\ &\,\downarrow \text{（第２項を展開）} \\ &= \sum_{n=1}^N [ \cancel{y^{(n)}\log(1+\exp(-\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)}))} + (1-y^{(n)})\boldsymbol{w}^\mathsf{T}\boldsymbol{x}^{(n)} + \log (1 + \exp(-\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)})) \cancel{-y^{(n)}\log (1 + \exp(-\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)}))} ] \\ &= \sum_{n=1}^N \underbrace{[ (1-y^{(n)})\boldsymbol{w}^\mathsf{T}\boldsymbol{x}^{(n)} + \log (1 + \exp(-\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)})) ]}_{=\varepsilon^{(n)}(\boldsymbol{w})とおく}. \end{align*} \end{split}\]

( $\varepsilon$も$\epsilon$と同じepsilonです)

上式を$ \boldsymbol{w}$で偏微分したいわけですが、少々煩雑できので、合成関数の微分（チェインルール, Chain Rule）を用いることにします。

$u^{(n)}= \boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}^{(n)}$として次式へ分解します。

\[\begin{split} \begin{align} \frac{\partial J(\boldsymbol{w})}{\partial \boldsymbol{w}} &= \frac{\partial}{\partial \boldsymbol{w}} \sum_{n=1}^N [(1-y^{(n)})\boldsymbol{w}^\mathsf{T}\boldsymbol{x}^{(n)} + \log (1 + \exp(-\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)}))] \\ &\,\downarrow \text{簡単のために}\varepsilon^{(n)}(\boldsymbol{w})= (1-y^{(n)})\boldsymbol{w}^\mathsf{T}\boldsymbol{x}^{(n)} + \log (1 + \exp(-\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)}))\text{を代入} \\ &= \frac{\partial}{\partial \boldsymbol{w}} \sum_{n=1}^N \varepsilon^{(n)}( \boldsymbol{w}) \\ &\,\downarrow \sum\text{を偏微分の外に追い出す}\\ &= \sum_{n=1}^N \frac{\partial \varepsilon^{(n)}(\boldsymbol{w})}{\partial \boldsymbol{w}} \\ &\,\downarrow \text{ここでチェインルールが登場}\\ &= \sum_{n=1}^N \frac{\partial \varepsilon^{(n)}}{\partial u^{(n)}} \frac{\partial u^{(n)}}{\partial \boldsymbol{w}}.\label{eq:chain} \end{align} \end{split}\]

チェインルールの左側の偏微分$\frac{\partial \varepsilon^{(n)}}{\partial u^{(n)}}$を計算します。
今、$\varepsilon^{(n)}(\boldsymbol{w})= (1-y^{(n)})\boldsymbol{w}^\mathsf{T}\boldsymbol{x}^{(n)} + \log (1 + \exp(-\boldsymbol{w}^\mathsf{T}\boldsymbol{x}^{(n)}))$より、

\[\begin{split} \begin{align} \frac{\partial \varepsilon^{(n)}}{\partial u^{(n)}} &= \frac{\partial}{\partial u^{(n)}} [ (1-y^{(n)})u^{(n)} + \log (1 + \exp(-u^{(n)})) ] \\ &= (1-y^{(n)}) – \frac{\exp(-u^{(n)})}{1 + \exp(-u^{(n)})} \\ &= (1 – \frac{\exp(-u^{(n)})}{1 + \exp(-u^{(n)})}) – y^{(n)} \\ &= \frac{1}{1 + \exp(-u^{(n)})} – y^{(n)} \\ &\,\downarrow \textstyle{(ロジスティック関数の式が出てきたからp^{(n)} = \frac{1}{1+\exp(-u^{(n)})}を代入)} \\ &= p^{(n)} – y^{(n)}.\label{eq:pd_epsilon} \end{align} \end{split}\]
チェインルールの右側の偏微分$\frac{\partial u^{(n)}}{\partial \boldsymbol{w}}$を計算します。
(ベクトルの掛け算、ここではただ掛け算が沢山並んでいるだけなので難しく考えないでOKです。) $$\begin{align} \frac{\partial u^{(n)}}{\partial \boldsymbol{w}} &= \frac{\partial (\boldsymbol{w}^\mathsf{T} \boldsymbol{x}^{(n)})}{\partial \boldsymbol{w}} \\ &= \boldsymbol{x}^{(n)}\ \ \because \text{(ベクトル微分の公式)}.\label{eq:pd_u} \end{align}$$

以上より以下が求まります。

\[ \begin{align} \frac{\partial J(\boldsymbol{w})}{\partial \boldsymbol{w}} = \sum_{n=1}^N (p^{(n)} – y^{(n)} ) \boldsymbol{x}^{(n)} \end{align} \]

どうせならforward propergationで出てくるものに変えたいのでPを入れる

最適なモデルパラメータの行列表記#

\[\begin{split} \underset{[N \times(F+1)]}{X}=\left(\begin{array}{ccccc} 1 & x_{1}^{(1)} & x_{2}^{(1)} & \cdots & x_{F}^{(1)} \\ 1 & x_{1}^{(2)} & x_{2}^{(2)} & \cdots & x_{F}^{(2)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{1}^{(N)} & x_{2}^{(N)} & \cdots & x_{F}^{(N)} \end{array}\right) \end{split}\]

\[\begin{split} \underset{[N \times 1]}{\boldsymbol{y}}=\left(\begin{array}{c} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{N)} \end{array}\right), \quad \underset{[N \times 1]}{\boldsymbol{p}}=\left(\begin{array}{c} p^{(1)} \\ p^{(2)} \\ \vdots \\ p^{(N)} \end{array}\right) \end{split}\]

\[ \frac{\partial J(\boldsymbol{w})}{\partial \boldsymbol{w}}=\left(\frac{\partial J}{\partial w_{0}}, \frac{\partial J}{\partial w_{1}}, \frac{\partial J}{\partial w_{2}}, \ldots, \frac{\partial J}{\partial w_{p}}\right)^{\mathrm{\top}} \]

\[\begin{split} \frac{\partial J(\boldsymbol{w})}{\partial \boldsymbol{w}}=\left(\begin{array}{c} \frac{\partial J}{\partial w_{0}} \\ \frac{\partial J}{\partial w_{1}} \\ \frac{\partial J}{\partial w_{2}} \\ \vdots \\ \frac{\partial J}{\partial w_{F}} \end{array}\right)=\underbrace{\left(\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ x_{1}^{(1)} & x_{1}^{(2)} & \cdots & x_{1}^{(N)} \\ x_{2}^{(1)} & x_{2}^{(2)} & \cdots & x_{2}^{(N)} \\ \vdots & \vdots & \ddots & \vdots \\ x_{F}^{(1)} & x_{F}^{(2)} & \cdots & x_{F}^{(N)} \end{array}\right)}_{=X^{\top}} \underbrace{\left(\begin{array}{c} p^{(1)}-y^{(1)} \\ p^{(2)}-y^{(2)} \\ \vdots \\ p^{(N)}-y^{(N)} \\ {[N \times 1]} \end{array}\right).}_{=\boldsymbol{p}-\boldsymbol{y}} \end{split}\]

ロジスティック回帰の実装#

TODO:

学習中のロスの可視化
学習中の境界の推移の可視化
irisの箱ひげ、pairplot

class LogisticRegression:
    """ロジスティック回帰実行クラス

    Attributes
    ----------
    eta : float
        学習率
    epoch : int
        エポック数
    random_state : int
        乱数シード
    is_trained : bool
        学習完了フラグ
    num_samples : int
        学習データのサンプル数
    num_features : int
        特徴量の数
    w : NDArray[float]
        パラメータベクトル
    costs : NDArray[float]
        各エポックでの損失関数の値の履歴

    Methods
    -------
    fit -> None
        学習データについてパラメータベクトルを適合させる
    predict -> NDArray[int]
        予測値を返却する
    """
    def __init__(self, eta=0.01, n_iter=50, random_state=42):
        self.eta = eta
        self.n_iter = n_iter
        self.random_state = random_state
        self.is_trained = False

    def fit(self, X, y):
        """
        学習データについてパラメータベクトルを適合させる

        Parameters
        ----------
        X : NDArray[NDArray[float]]
            学習データ: (num_samples, num_features)の行列
        y : NDArray[int]
            学習データの教師ラベル: (num_features, )のndarray
        """
        self.num_samples = X.shape[0]  # サンプル数
        self.num_features = X.shape[1]  # 特徴量の数
        # 乱数生成器
        rgen = np.random.RandomState(self.random_state)
        # 正規乱数を用いてパラメータベクトルを初期化
        self.w = rgen.normal(loc=0.0, scale=0.01, size=1+self.num_features)
        self.costs = []  # 各エポックでの損失関数の値を格納する配列
        # パラメータベクトルの更新
        for _ in range(self.n_iter):
            net_input = self._net_input(X)
            output = self._activation(net_input)
            # 式(2)
            self.w[1:] += self.eta * X.T @ (y - output)
            self.w[0] += self.eta * (y - output).sum()
            # 損失関数: 式(1)
            cost = (-y @ np.log(output)) - ((1-y) @ np.log(1-output))
            self.costs.append(cost)
        # 学習完了のフラグを立てる
        self.is_trained = True

    def predict(self, X):
        """
        予測値を返却する

        Parameters
        ----------
        X : NDArray[NDArray[float]]
            予測するデータ: (any, num_features)の行列

        Returens
        -----------
        NDArray[int]
            0 or 1 (any, )のndarray
        """
        if not self.is_trained:
            raise Exception('This model is not trained.')
        return np.where(self._activation(self._net_input(X)) >= 0.5, 1, 0)

    def _net_input(self, X):
        """
        データとパラメータベクトルの内積を計算する

        Parameters
        --------------
        X : NDArray[NDArray[float]]
            データ: (any, num_features)の行列

        Returns
        -------
        NDArray[float]
            データとパラメータベクトルの内積の値
        """
        return X @ self.w[1:] + self.w[0]

    def _activation(self, z):
        """
        活性化関数（シグモイド関数）

        Parameters
        ----------
        z : NDArray[float]
            (any, )のndarray

        Returns
        -------
        NDArray[float]
            各成分に活性化関数を適応した (any, )のndarray
        """
        return 1 / (1 + np.exp(-np.clip(z, -250, 250)))

import plotly.express as px
iris_df = px.data.iris()

iris_pairplot = px.scatter_matrix(
    iris_df, 
    dimensions=["sepal_width", "sepal_length", "petal_width", "petal_length"],
    color="species",
    width=800,height=800,
)
iris_pairplot.show()

from sklearn.preprocessing import StandardScaler

# 標準化のインスタンスを生成（平均=0, 標準偏差=1 に変換）
sc = StandardScaler()
X = sc.fit_transform(iris_df.iloc[:,:4].values)

from sklearn.model_selection import train_test_split
y = iris_df.species_id
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=10, stratify=y)

# ロジスティック回帰モデルの学習
lr = LogisticRegression(eta=0.5, n_iter=1000, random_state=3)
lr.fit(X_train, y_train)

get_acc = lambda X,y: (lr.predict(X) == y).sum() / y_test.shape[0]
print("テスト正答率:",get_acc(X_test, y_test))

テスト正答率: 0.03333333333333333

lr.predict(X_train)

print("テスト正答率:",get_acc(X_train, y_train))

テスト正答率: 0.16666666666666666